Super Short Introduction
- Paper Link
- This work of mine solves the problem of estimating gaze of a person in unconstrained environments - variable camera-person distance and full \(360^\circ\) variation in Yaw. Variable camera-person distance is handled via a multi-scale approach where features from multiple scales are aggregated. A full \(360^\circ\) variation in Yaw raises an interesting problem of predicting backward gazes which is improved upon by using a weighted sine-cosine transformation.
An Overview of the Methodology
Definitions:
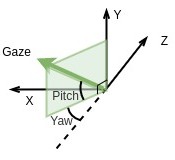
- Yaw \(\theta\) and Pitch \(\phi\) angle: In polar co-ordinates a normalized 3D vector can be represented by 2 angles. Gaze vector is therefore represented by \(\theta\) (left right orientation) and \(\phi\) (top down orientation).
Sine-Cosine Transformation
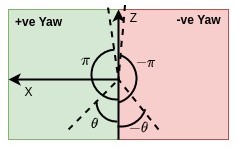
Backward gaze induces discontinuity at \(\theta=\pm\pi\) as seen in figure below. Yaw angle is defined with respect to negative z axis. Discontinuity is seen when the projection of gaze vector on XZ plane is very close to positive Z direction. From one side the angle reaches \(\pi(3.14)\) and from the other, it reaches \(-\pi(-3.14)\).
We solve the issue by applying sine-cosine transformation on target - we predict \(sin(\theta)\), \(cos(\theta)\) and \(sin(\phi)\).
It is easy to see that in sine-cosine space, there is no discontinuity at \(\theta=\pm\pi\). We predict \(\theta\) from two ways. We estimate Sine-based estimate \(\theta_S\) by using predicted \(sin(\theta)\) and sign of \(cos(\theta)\). We obtain Cosine-based estimate \(\theta_C\) by using predicted \(cos(\theta)\) and sign of \(\sin(\theta)\). Our prediction for yaw is \(\theta_{SC} = (\theta_S + \theta_C\))/2
Weighted Sine-Cosine Transformation
We observe that \(\theta_C\) is not able to predict \(0^\circ\) and \(\theta_S\) is not able to predict \(\pm\pi/2\) as can be seen in below figure where we look at their distributions.
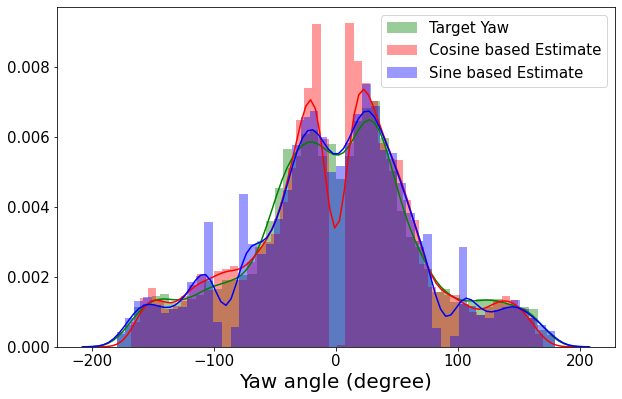
We argue that it is due to low derivative of \(tanh\) around \(\pm1\) and high derivative of \(sin^{-1}\) and \(cos{-1}\) around \(\pm\pi/2\) and \(0^\circ\) respectively. We fix this by using a weighted average scheme. Our final prediction for yaw,
\[\theta_{WSC} = w*sin(\theta) + (1-w)*cos(\theta)\]Finally, we note that there is no ambiguity in estimating \(\phi\) from \(sin(\phi)\) since \(\phi \in [-\pi/2,\pi/2]\)
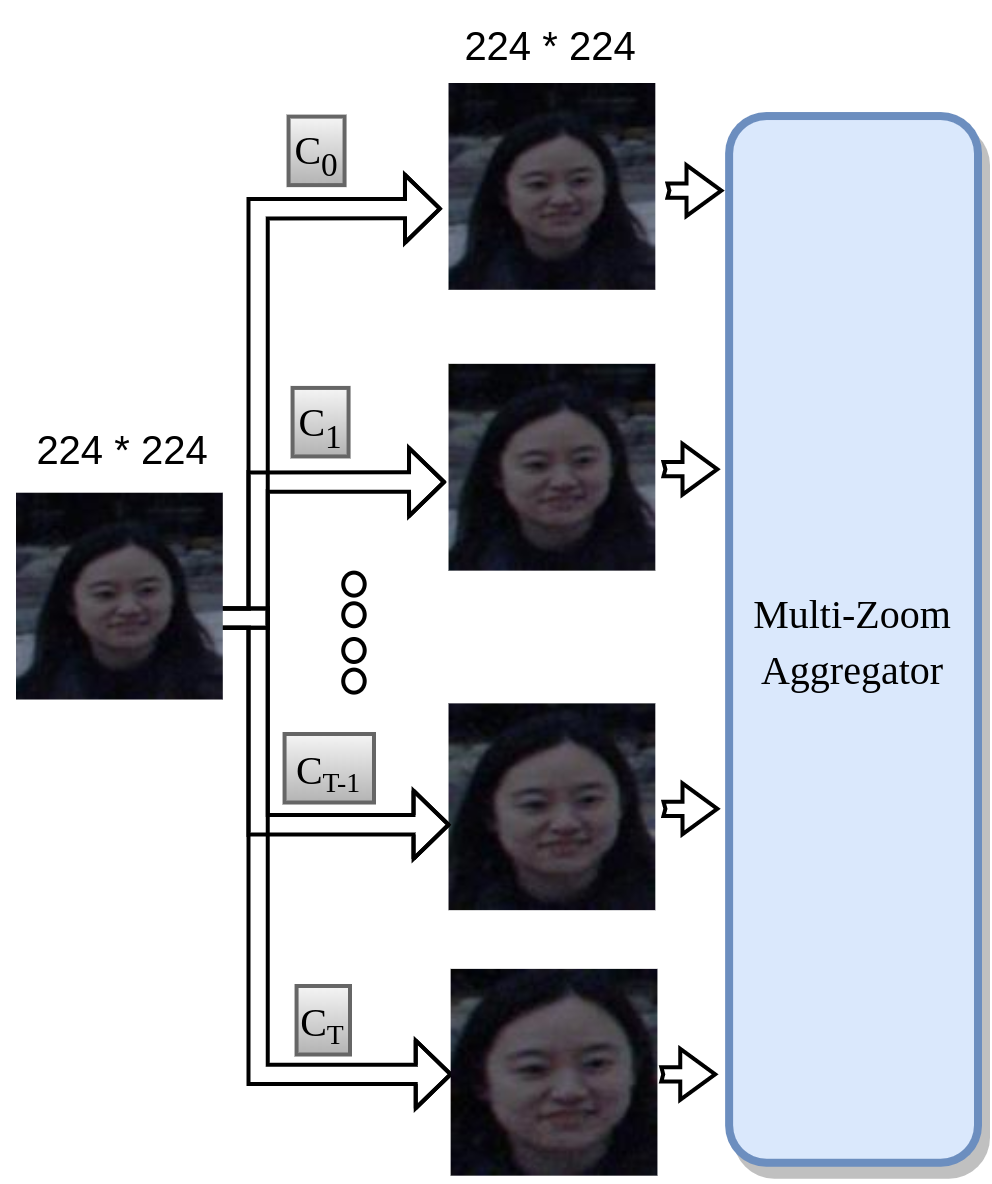
Multi-Crop Approach
We take this approach to do efficient feature extraction over varying head sizes appearing in the dataset as shown below.

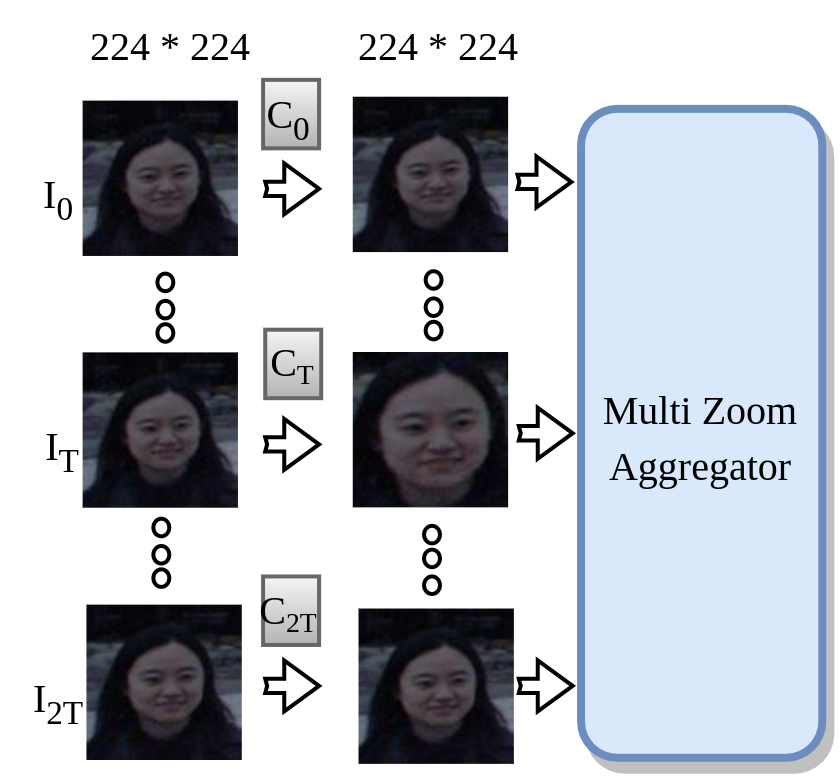
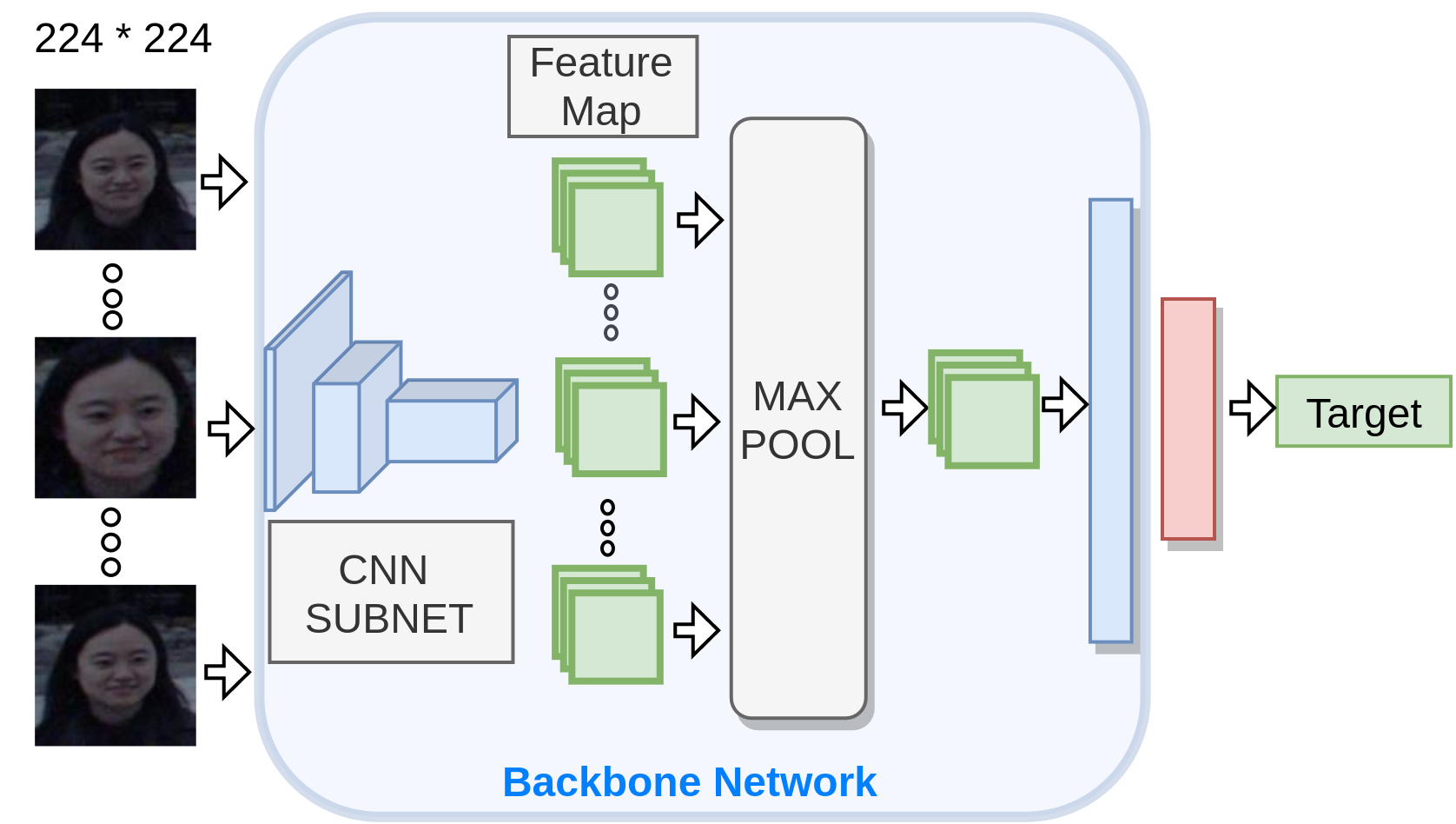
We use multiple cropsizes. We centercrop the input image with each cropsize and resize it subsequently. This yields a set of images with different scales. We then pass it through a common backbone network to yeild multi-scale embeddings. These embeddings are aggregated using an aggregation module and subsequently passed though dense layer to yield the target. For sequence model (using video as input), instead of a single input, we have multiple input images and we apply one centercropping operation to each input. Subsequent portions are identical.