Dual Resolution Corresponding Networks

Super Short Introduction

• Paper Link
• This paper solves the problem of finding correspondences between two images (aka does keypoint matching) by using 2 feature maps of different resolutions. Less compute requirements and more robust keypoint matching are the major benefits of this approach.

Understanding the Paper

Relevant Background

A popular method of establishing correspondences relevant to this paper involves a 3 stage pipeline:

1. Detection: Detect potential keypoints in both images. Technically speaking, this is a list of (x,y) coordinates.
2. Description: For every position detected in step 1, get a feature embedding of the surrounding region. One can for example use 32*32 region centered on the given position and use first few layers of the pretrained resnet18 to get feature embedding for that position.
3. Matching: Compute a similarity metric (correlation is used in this paper) between the descriptions of positions of the two images to come up with correspondances.

Missing Detection Problem is a prominent issue plaguing this approach. It can happen that some relevant keypoints are not detected in the detection phase. To solve missing detection, one can use all positions of image. Using CNNs, it is possible to generate the descriptions for all positions in one pass as has been done in NCNet. However, computing correspondences becomes expensive as one needs to find correlation between each possible position pair of the two images.

What has been Done in the Paper:

Like NCNet, they have made use of a 4D tensor for storing correlation between all possible position pairs. Doing this, they have taken care of missing detection problem.

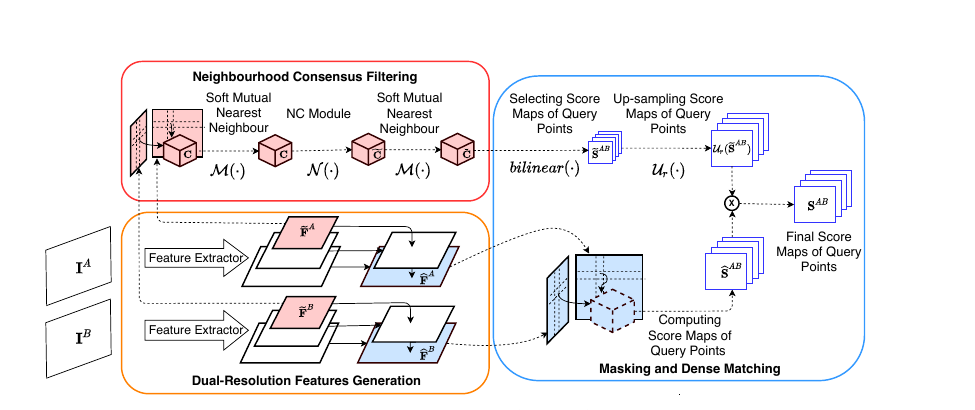
To make the model compute efficient, they have used two resolutions for keypoint Description. They compute the full 4D correlation tensor using the low resolution descriptions aka feature map \(\tilde{F}\). Let us name the two images as A and B and their low resolution descriptions as \(\tilde{F_A}\) and \(\tilde{F_B}\). For every position \((i_A,j_A)\) in \(\tilde{F_A}\) and every position \((i_B,j_B)\) in \(\tilde{F_B}\), the 4D correlation tensor has a corresponding entry storing the correlation between their descriptions. Then, similar to NCNet, they use a neighborhood consensus module to refine the correlation tensor. This refinement essentially reduces the score for outlier matches.

Using this refined correlation, they know relevant keypoints in low resolution. They upscale it to match the higher resolution feature map. Those keypoints now map to localized regions in higher resolution feature map. So, this upscaled refined correlation has localized regions which can have potential keypoints. Only for these regions, they compute the correlation using higher resolution feature maps, \(\hat{F}\). This is where they get their speedup as they did not compute the full 4D correlation tensor on higher resolution feature maps.

The measure of correspondence between the two points is the product of \(\hat{F}\) and refined and upscaled \(\tilde{F}\). Since this measure takes into account two scales, it is claimed to be more robust as is evident by its superior performance on multiple benchmarks.